-
This forum contains old posts that have been closed. New threads and replies may not be made here. Please navigate to the relevant forum to create a new thread or post a reply.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
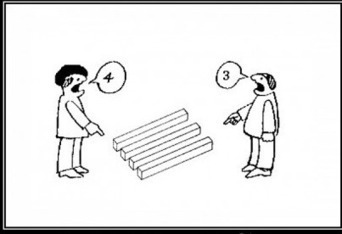
3 or 4 ?
- Thread starter P.J.
- Start date
- Status
- Not open for further replies.
Raji Ram
Active member
Mathematical proof is possible for the above drawing!
If the number of planks drawn in the left side is taken as 'n', the number of planks in the right side is 'n-1'
We need 2n+1 lines in total, to draw 'n' planks in the left side and three lines for EACH of the planks on the right.
The equation to find 'n' is:
2n +1 = 3 X (n-1) since we need 3 lines to represent a plank in the right side.
2n + 1 = 3n - 3
changing sides
3n - 2n = 1 + 3
Hence n = 4.
That is why four planks are shown in the left side and three on the right!

If the number of planks drawn in the left side is taken as 'n', the number of planks in the right side is 'n-1'
We need 2n+1 lines in total, to draw 'n' planks in the left side and three lines for EACH of the planks on the right.
The equation to find 'n' is:
2n +1 = 3 X (n-1) since we need 3 lines to represent a plank in the right side.
2n + 1 = 3n - 3
changing sides
3n - 2n = 1 + 3
Hence n = 4.
That is why four planks are shown in the left side and three on the right!
S
SANDHYAV
Guest
1. We need 2n+1 lines in total, to draw 'n' planks in the left side and three lines for EACH of the planks on the right.
The equation to find 'n' is:
2. 2n +1 = 3 X (n-1) since we need 3 lines to represent a plank in the right side.
1. how
2. why 3 times n-1
Raji Ram
Active member
1. We have taken 'n' as the number of planks in the LHS. Here, only the first plank needs three lines and the following have two more EACH.
1. We need 2n+1 lines in total, to draw 'n' planks in the left side and three lines for EACH of the planks on the right.
The equation to find 'n' is:
2. 2n +1 = 3 X (n-1) since we need 3 lines to represent a plank in the right side.
1. how
2. why 3 times n-1
Thus we need 3 + 2 + 2 and so on to draw in that manner. All the planks after the first need ONLY two lines. So total lines are 2n + 1 OK?
We have one plank LESS on the right hand side. Since the number of planks on LHS is denoted by 'n' the number on the RHS will be (n - 1)
Hope it is clear up to this.
2. We need three lines to denote EACH plank on the RHS. So, we have to multiply the number of planks in RHS by 3 to get the number of lines.
Since the lines drawn are the SAME for planks on LHS and RHS, we equate 2n + 1 and 3 x (n - 1) :thumb:
S
SANDHYAV
Guest
haha,
only horizontal lines !
also this 4-3 combination is possible only for 4-3 and not for 5-4
only horizontal lines !
also this 4-3 combination is possible only for 4-3 and not for 5-4
Raji Ram
Active member
YES! In fact ONLY for 4 and 3 if drawn in this way! :decision:haha,
only horizontal lines !
also this 4-3 combination is possible only for 4-3 and not for 5-4
prasad1
Active member
I agree with Rajiji,The drawing is wrong!
Check out the lines starting from the left side!
The 2nd z-axis line are wrong.
The 3rd Y-axis line is wrong.
P.J.
0
Are you not a math student P J Sir?
It is a very simple calculation.
Raji Madam
No...... I took only General Mathematics
Verala uttu kootra case illa , better than that !!
- Status
- Not open for further replies.